錯視(目の錯覚)とは
視覚において、実際のものとは異なるものとして知覚されること。
人は、網膜像をそのまま知覚しているのではなく、脳内で解釈・推論などによって修正されている。
物理的には正しいデザインでも、錯視によっておかしく見えてしまうことがあるため、錯視を考慮してデザインすることもある。
錯視には、形の錯視(幾何学的錯視)、色の錯視、運動の錯視などがある。
形の錯視(幾何学的錯視)
大きさ、方向、湾曲などの形に関わる錯視である。
以下は、形の錯視(幾何学的錯視)の例。
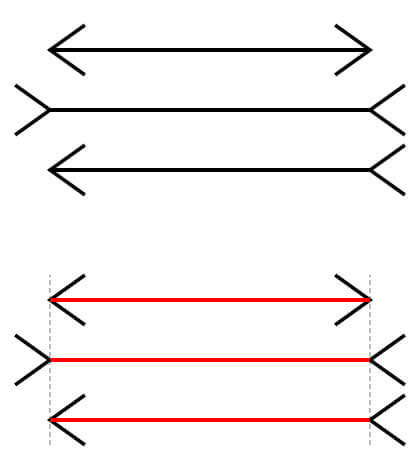
ミュラー・リヤー錯視(大きさの錯視)
線の両端に矢印(<ー>)を描くと、線が短く見える。
線の両端に矢印の逆向き(>ー<)を描くと、線が長く見える。
実際には、どちらも同じ長さの線である。
詳しい説明(解説)は、以下をご覧ください。
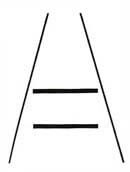
ポンゾ錯視(大きさの錯視)
三角形のような斜めの線があるとき、横向きの二つの線は上に行くほど長く見える。
実際には、どちらも同じ長さの線である。
詳しい説明(解説)は、以下をご覧ください。
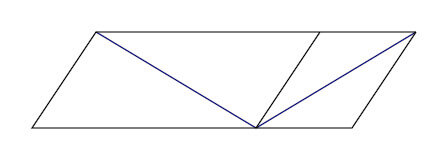
ザンダー錯視(大きさの錯視)
大きさの異なる平行四辺形において、対角線の長さが違って見える。
左側の平行四辺形の対角線のほうが、右側の平行四辺形の対角線より長く見える。
実際には、どちらも同じ長さの線である。
ツェルナー錯視(方向の錯視)
長い線はすべて並行であるが、斜めに描かれた短い線によって、実際よりも傾いているように見える。

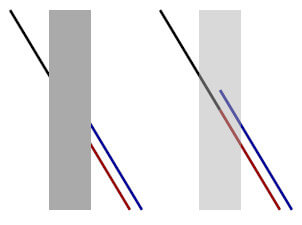
ポゲンドルフ錯視(方向の錯視)
直線の一部がさえぎられて見えないとき、線は直線ではなく、少しずれて見える。
以下の図で、左の画像を見ると、黒い線とつながっているのは青い線に見える。
しかし、右の画像を見るとわかる通り、黒い線は赤い線とつながっている。
ヘリング錯視(湾曲の錯視)
縦向きの二つの並行した線は、実際には直線であるが、背景の線によって凸レンズのように湾曲して見える。
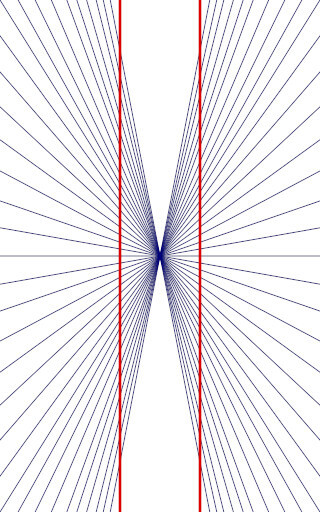
ヴント錯視(湾曲の錯視)
ヘリング錯視の逆バージョンで、縦向きの二つの直線が、背景の線によって凹レンズのように湾曲して見える。
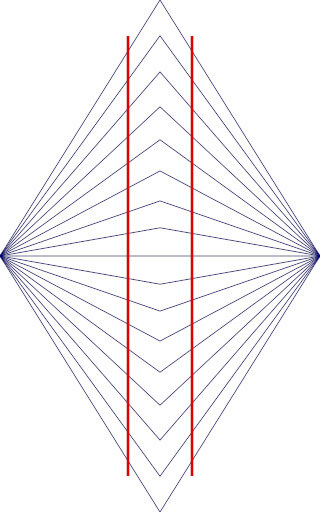
カフェウォール錯視(方向の錯視)
白い四角形と黒い四角形を少しずらして交互に並べると、横方向の境界線が傾いて見える。

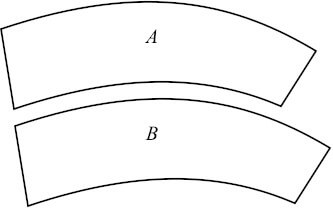
ジャストロー錯視(大きさの錯視)
扇型を二つ並べると、外側(A)よりも内側(B)のほうが大きく見える。
実際には、どちらも同じ大きさの扇型である。
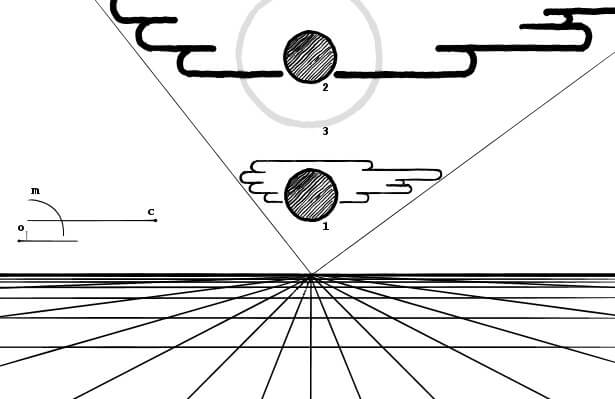
デルブーフ錯視(大きさの錯視)
左図のように、黒丸に大きい同心円を描くと、黒丸はより小さく見える。
右図のように、黒丸に小さい同心円を描くと、黒丸はより大きく見える。
実際には、どちらも同じ大きさの丸である。

エビングハウス錯視(大きさの錯視)
左図のように、中心(オレンジ色)の丸の周囲に大きい丸を配置すると、中心の丸はより小さく見える。
右図のように、中心(オレンジ色)の丸の周囲に小さい丸を配置すると、中心の丸はより大きく見える。
実際には、どちらも同じ大きさの丸である。

反転図形・多義図形による錯視
反転図形・多義図形も錯視とされることがある。
遠近などの反転に関わる錯視である。
以下は、反転図形・多義図形による錯視の例。
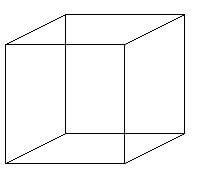
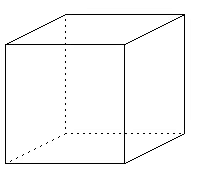
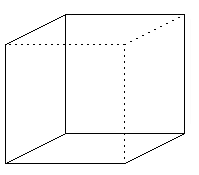
ネッカーの立方体(反転の錯視)
前面の線と後面の線がどちらも見えているため、どちらが前かわからない。(左図)
そのため、点線のような二つの見方ができるようになっている。(右二つ)
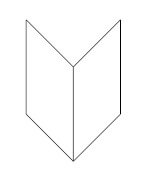
マッハの本(反転の錯視)
遠近感が不明のため、本が手前に折れているのか、奥に折れているのかがわからない。
本が手前に折れている場合は、カバー(表紙)が見えており、読む人が奥にいることになる。
本が奥に折れている場合は、中身(文章)が見えており、読む人が手前にいることになる。
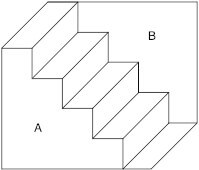
シュレーダーの階段(反転の錯視)
A面が手前、B面が奥だとすると、右下から左上に上がる階段のように見える。
A面が奥、B面が手前だとすると、階段が天井に逆さまについているかのように見える。
不可能図形・矛盾図形・逆理図形による錯視
不可能図形・矛盾図形・逆理図形も錯視とされることがある。
2次元で描くことはできても、3次元の現実では不可能な図形による錯視である。
以下は、不可能図形・矛盾図形・逆理図形による錯視の例。
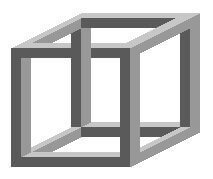
不可能の立方体(不可能の錯視)
反転図形の両方の要素が含まれているため、現実(3次元)には不可能である。
エッシャーの『物見の塔』については、以下をご覧ください。
ペンローズの三角形(不可能の錯視)
立体の影になるところが立体の前面にもなっているため、現実(3次元)には不可能である。

詳しい説明(解説)は、以下をご覧ください。
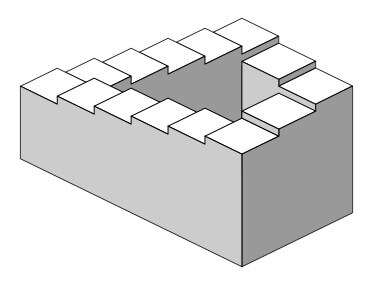
ペンローズの階段(不可能の錯視)
ずっと上り続ける(下り続ける)階段になっているため、現実(3次元)には不可能である。
エッシャーの『上昇と下降』については、以下をご覧ください。
エッシャーの滝(不可能の錯視)
ずっと流れ続ける水路になっているため、現実(3次元)には不可能である。

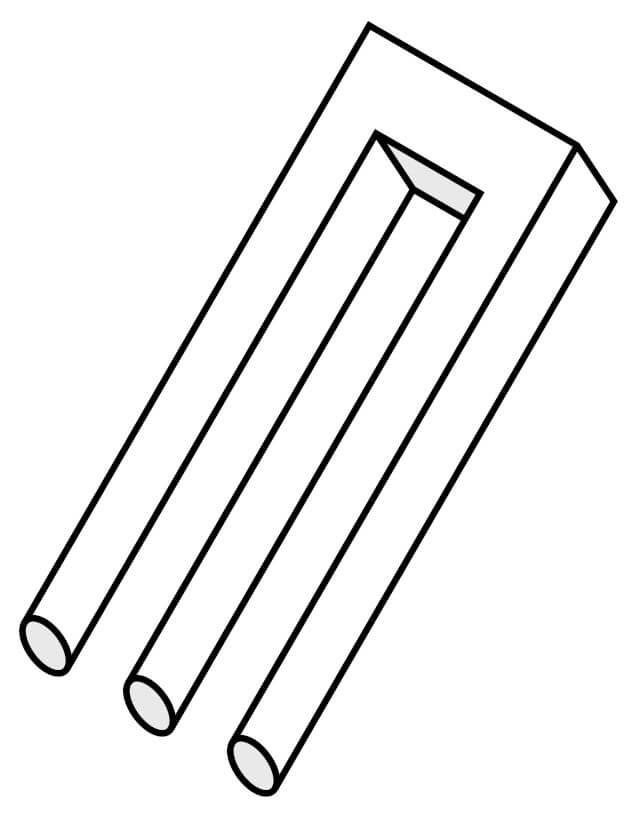
ブリヴェット・悪魔のフォーク(不可能の錯視)
円柱が途中で角柱に変わっており、図(ず)と地(じ)にもずれが生じているため、現実(3次元)には不可能である。
色の錯視・明るさの錯視
色、明るさに関わる錯視である。
以下は、色・明るさの錯視の例。
ハーマングリッド・ヘルマン格子錯視(色・明るさの錯視)
格子状の図形で、白線の交差部分に黒い影が見える。

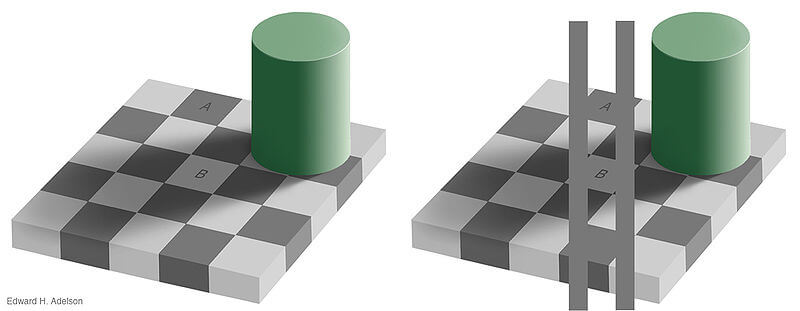
チェッカーシャドウ錯視(色・明るさの錯視)
円柱の影になっていないタイル(A)は、より黒く見える。
円柱の影になっているタイル(B)は、より白く見える。
実際には、どちらも同じ色・明るさのタイルである。(右図)
運動の錯視
静止画なのに動いて見える錯視である。
以下は、運動の錯視の例。
蛇の回転(運動の錯視)
蛇がトグロを巻いたような図形が勝手に動いているように見える。

そのほか
そのほかにも一般的に知られている錯視がある。
月の錯視
月が空高くあるときよりも、地平線や水平線に近くあるときのほうが大きく見える。
スピニング・ダンサー(シルエット錯視)
動画のシルエット錯視。
シルエットを見ただけでは、右回りに回転しているのか、左回りに回転しているのかわからない。
軸足が右足だとすると、上から見下ろして左回り(反時計回り)に回転しているように見える。
軸足が左足だとすると、上から見下ろして右回り(時計回り)に回転しているように見える。

よりわかりやすい説明(動画)は、以下をご覧ください。
彼は行くのか?来るのか?(シルエット錯視)
静止画のシルエット錯視。
シルエットを見ただけでは、向こうに向かっているのか、こちらに近づいているのかがわからない。

参考
関連する心理学用語
ゲシュタルト


コメント