ミュラー・リヤー錯視（ミュラー・リヤーの図形）

ミュラー・リヤー錯視（ミュラー・リヤーの図形）とは

線などに関する大きさ（長さ）の錯視（幾何学的錯視）の図形。

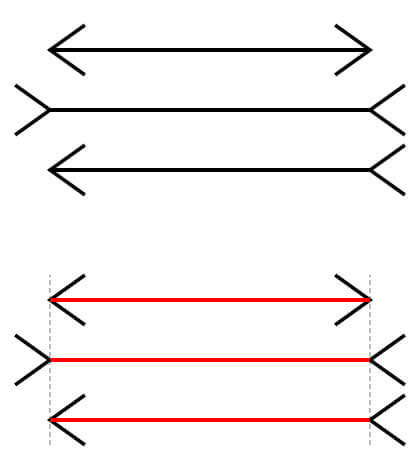
線の両端に矢印（＜ー＞）を描くと、線が短く見える。

線の両端に矢印の逆向き（＞ー＜）を描くと、線が長く見える。

実際には、どちらも同じ長さの線である。

https://commons.wikimedia.org/wiki/File:M%C3%BCller-Lyer_illusion.svg

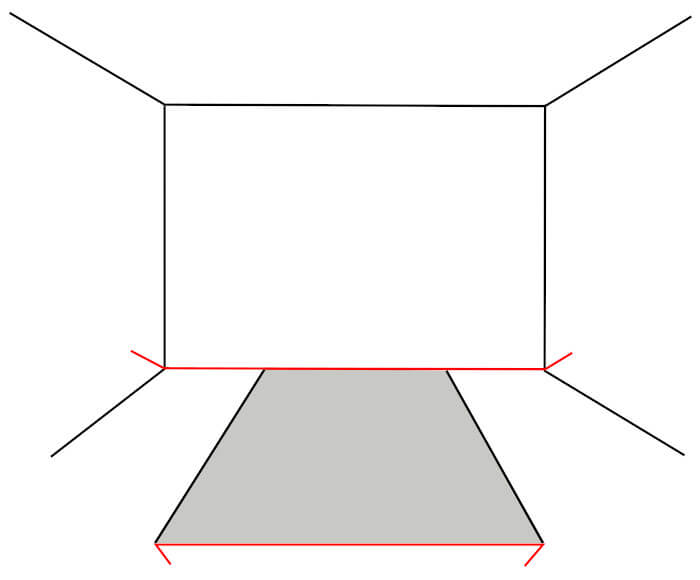
ミュラー・リヤー錯視は、脳における遠近感の解釈・推論によって説明される。

以下の図のように、線の両端に矢印の逆向き（＞ー＜）があると遠方であることが多い。

逆に、線の両端に矢印（＜ー＞）があると近くであることが多い。

このため、遠方の線はより長く、近くの線はより短いものだと推論しているのである。

https://commons.wikimedia.org/wiki/File:Mueller_lyer.svg

そのほかの錯視については、以下をご覧ください。

有斐閣